저번 시간에 우리는 거리 정보 중 단축을 다루었습니다.
1점 투시는 그 중 한쪽 방향으로의 단축을 그리는 것이었습니다.
- 두 방향으로의 단축, 2점 투시
저번 시간에 지평선은 소실점의 모임이라고 생각해도 좋다는 이야기를 했었습니다. 기억나시나요? 이게 진가를 발휘할 시간입니다.
→ 지평선 위에서 두 소실점을 잡으면 2점 투시가 된다!
임의로 적당히 떨어진 점 두 개를 잡고 어느 선들이 평행한지 생각하며 직사각형을 그려 봅시다.
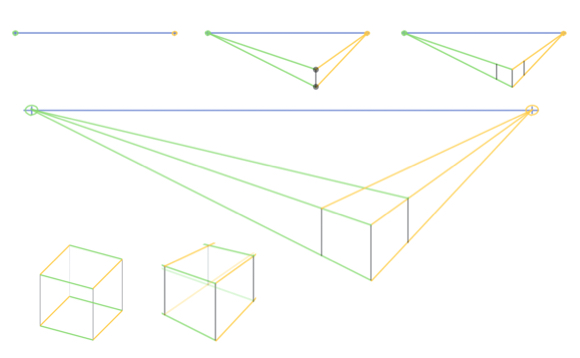
(더 생각해 봅시다 : 두 점에서 나오는 선들이 수직이어야 2점 투시 위의 직사각형이 되겠죠? 그건 어떻게 알까요? → 데이비드 첼시의 만화로 배우는 투시원근법의 심화 내용 참조)
선을 몇 개 더 그어서 여러 직사각형을 그려 봅시다.
이번에도 눈높이와 직사각형의 관계에 집중해 봅니다. 밑면이 보이는 직사각형이 (눈높이 = 지평선)위에 올바르게 존재하나요? 윗면이 보이는 정사각형이 눈높이 아래에 존재하나요? 옆면이 보이는 직사각형이 눈높이에 존재하나요?
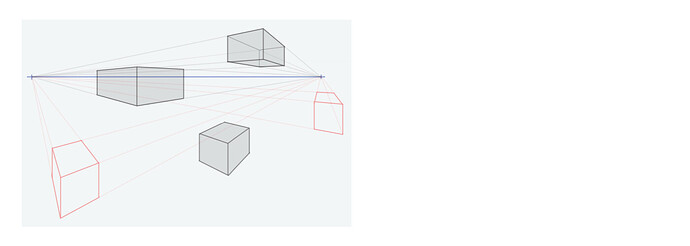
- 또 2점 투시에서 주의해야 할 점은 아래 사진에서 빨간색으로 그려진 직사각형입니다.
좀 많이 찌그러져 있죠? 이들은 왜곡이 심하게 이루어졌다고 부르는 녀석들입니다. 얘네들은, 소실점 가까이에 있기 때문에 단축이 많이 일어나 형태가 얼그러집니다.
→ 2점 투시를 이용할 때는 소실점에서 적당히 떨어진 곳을 화면에 잡는 것이 좋습니다.
실제로, 보통 그림을 보면
이렇게 소실점이 그림 밖으로 나가게 하는 경우가 많습니다. 그래야 안정적으로 화면 속에 물체가 담기거든요.
- 1점 투시를 2점 투시로 나누는 법, 대각소실점
정말 2점 투시에서 소실점을 어떻게 잡아야 할지 모르겠다! 하는 분들을 위한 일종의 꼼수입니다.
1점 투시로 정육면체를 그려줍니다. (정확한 정육면체를 그리는 방법은 상당히 복잡하나, 눈에 보이기에 정육면체인 정도여도 됩니다.)
그림과 같이 대각선을 쭉 이어서 지평선에 소실점 두 개를 찍어줍니다.
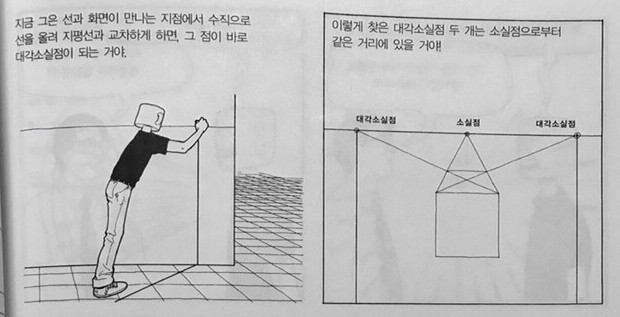
대각선으로 만들어진 대각소실점이니 두 직선이 직교하는 것은 금방 알 수 있겠죠? 이제 두 점으로 그림을 그리면 2점 투시도가 될 것입니다! 이렇게 1점 투시를 2점 투시로 나누는 방법도 있습니다.
-
유의하면서 아래와 같이 풍경 스케치를 해봅시다.

-
오늘의 결론
단축의 방향을 몇 개로 설정하냐 를 세는 것보다, 단축하는 직선 사이 관계를 생각하는 것이 중요합니다.
실제로는, 지평선 방향으로 나아가는 모든 물체는 단축이 일어나겠죠. 그중 적당한 직선을 찾아서 직각을 그리겠다가 원근법의 컨셉입니다. 개별의 물체가 개별의 평행한 직선을 가지면서 개별의 소실점을 가질 수도 있습니다.
그러다가, 하늘 방향으로 한번 더 단축시키면 3점 투시가 되는거에요.
그냥 그런 겁니다.
참 쉽죠?